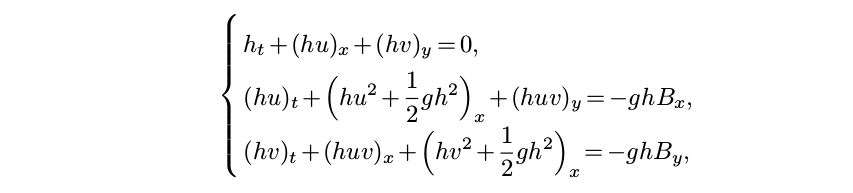Surface model (Water Overlay): Difference between revisions
No edit summary |
No edit summary |
||
| Line 34: | Line 34: | ||
* In addition to water flowing in between grid cells, water can also flow ''through'' [[Hydraulic structures (Water Overlay)|hydraulic constructions]]. | * In addition to water flowing in between grid cells, water can also flow ''through'' [[Hydraulic structures (Water Overlay)|hydraulic constructions]]. | ||
* The [[Design flood elevation m model attribute (Water Overlay)|DESIGN_FLOOD_ELEVATION_M]] attribute confines the maximum surface elevation induced by constructions. | * The [[Design flood elevation m model attribute (Water Overlay)|DESIGN_FLOOD_ELEVATION_M]] attribute confines the maximum surface elevation induced by constructions. | ||
==References== | ==References== | ||
Revision as of 08:59, 1 July 2019
Computation
The Water Module's primary function is simulating two-dimensional flow of water along the surface. In order to do this, the project area is first discretized into x by y cells depending on the configured grid cell size. Secondly, a set of rules is required that describes the behavior of the flow. This is done through a second-order semi-discrete central-upwind scheme produced by Kurganov and Petrova (2007)[1], which is based on the 2-D Saint-Venant equations (a.k.a. shallow water equations):
where
- ht = water depth at time t
- ut = velocity in the x direction at time t
- vt = velocity in the y direction at time t
- Bx = slope in the x direction
- By = slope in the y direction
- g = gravitational constant
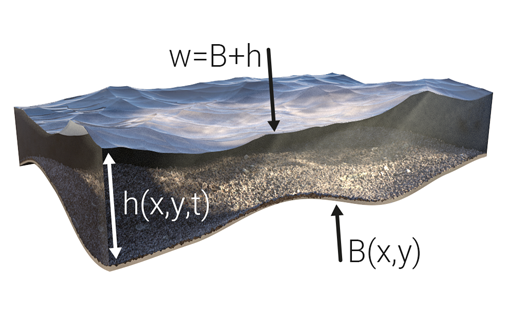
This scheme deviates from the original Saint-Venant equations in that it approaches the system in terms of water surface elevation (w = h + B) and flux (hu and hv), rather than just the water depth (h). The image on the right aims to clarify on the various terms. More technical information on the Tygron Platform's implementation of the Well-Balanced Positivity Preserving Central-Upwind Scheme can be found here.
Flowing water
Imbalances in the water surface elevation among grid cells drive the flow of water in the model until a state of equilibrium is reached in terms of w and flux.
Water level initialization
In theory, each grid cell can have a unique bottom elevation and accompanying water depth, yielding a certain water surface elevation (or water level). However, in practice, water levels are often initialized for large groups of cells, assuming that each (water level) area in a project has been assigned a water level. During the initialization phase a distinction is made between two types:
For all water terrains in a water level area, the volume of water per grid cell is such that the resulting water level at those locations conforms the value of the WATER_LEVEL attribute as provided by the corresponding water level area.
In contrast to water level areas, which generate water on water terrains, inundation areas generate water over all grid cells, regardless of its terrain type. Similarly, the volume of water per grid cell is determined by the INUNDATION_LEVEL attribute as provided by the corresponding inundation area.
If a grid cell is neither part of any water level area nor inundation area, or the assigned water level is lower than its bottom elevation, the water depth is assumed to be zero and the water level becomes equal to the bottom elevation. In turn, this bottom (or surface) elevation is equal to the local terrain height of the project area, though it may be altered by the presence of a construction or the BREACH_HEIGHT attribute of a breach.
Notes
- Water can be added to and removed from the described surface system by the rain, evaporation and infiltration model, as well as certain hydraulic structures and breaches.
- In the case of subsurface flow a different flow system with different equations are used.
- In addition to water flowing in between grid cells, water can also flow through hydraulic constructions.
- The DESIGN_FLOOD_ELEVATION_M attribute confines the maximum surface elevation induced by constructions.
References
- ↑ Kurganov A, Petrova G (2007) ∙ A Second-Order Well-Balanced Positivity Preserving Central-Upwind Scheme for the Saint-Venant System ∙ found at: http://www.math.tamu.edu/~gpetrova/KPSV.pdf (last visited 2019-04-11)