Sky view factor calculation model (Heat Overlay): Difference between revisions
| Line 43: | Line 43: | ||
With the sky view area, the sky view factor can be calculated by dividing the sky view area by the area of the circle of the horizontal plane. | With the sky view area, the sky view factor can be calculated by dividing the sky view area by the area of the circle of the horizontal plane. | ||
<math>\frac{\sum_{1}^n area_i }, \ | <math>\frac{\sum_{1}^n area_i }, \pi r^2 }</math> | ||
[[File:Sky_view_area.png|300px]] | [[File:Sky_view_area.png|300px]] | ||
Revision as of 14:56, 19 September 2019
Sky limiters
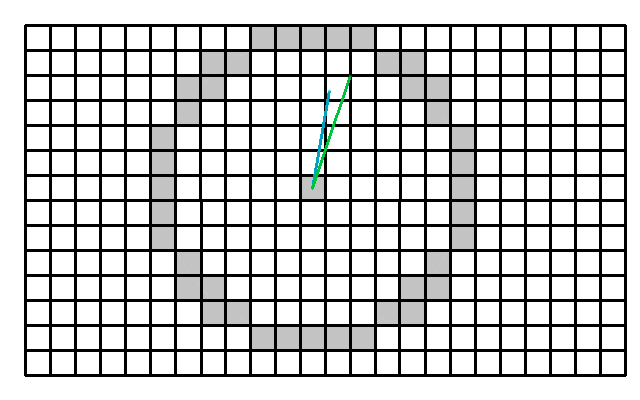
The model starts by determining per grid cell what the height of obstacles are on that grid cell. An obstacle can be:
- a building,
- foliage, such as trees; The top of foliage is used as the obstacle height;
- terrain height.
The sky view factor is calculated for the body height of 1.2 meters. This means that sky view is determined for a height of 1.2 above the surface height, which is with building but without foliage height.
Sky exposure factor versus sky view factor
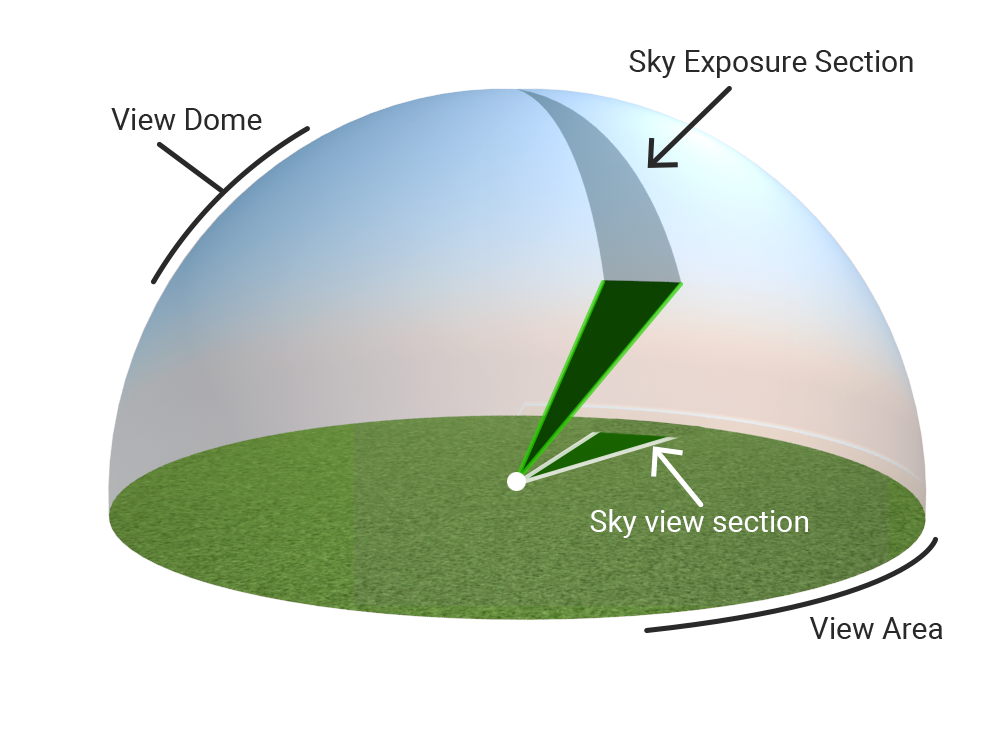
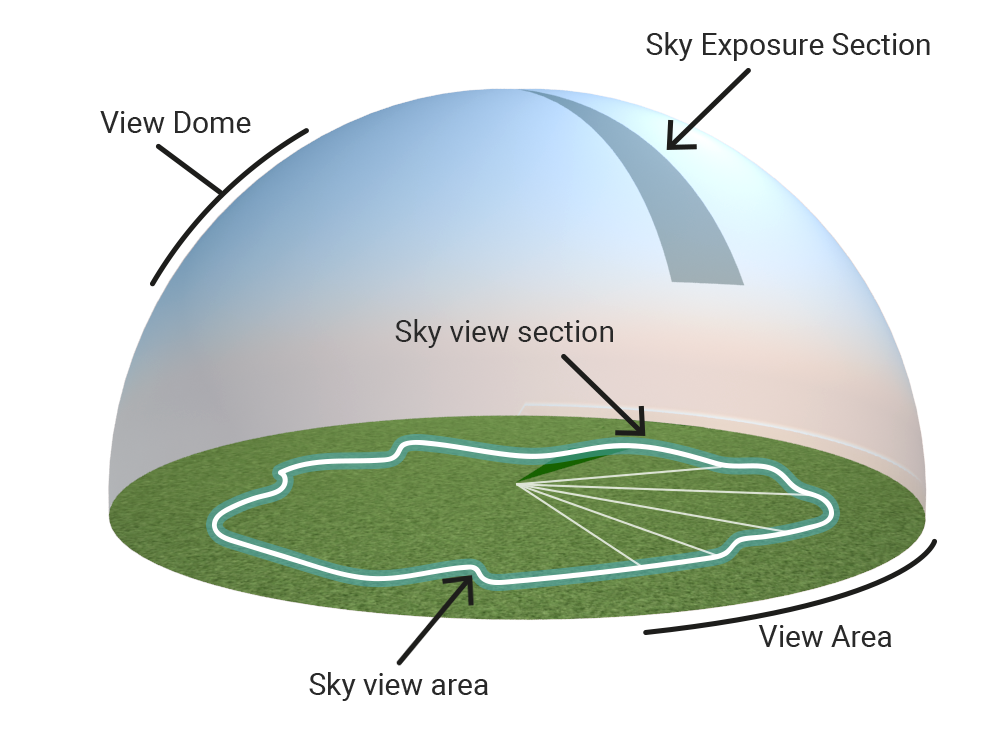
In literature, two sky parameters are mentioned that are sometimes confused: Sky exposure and sky view factor. The sky exposure is related to the sky view dome (3D). The sky view factor is related to the projection of the view dome to the horizontal plane. Here we call the projected circle the view circle. In the second image, you can distinguish a sky view section on the dome and a section projected on the view circle.
Why is the sky view factor selected?
The reason why the sky view factor is selected and not the sky exposure, is because the sky view factor result weights objects closer to the top of the sky view dome higher than objects further away. This is caused by the projection from 3D to 2D. And it is desirable, because the sky view factor is directly related to the reflected radiation in the used formula's.
Sky view factor
The area of a sky view section is calculated as followed:
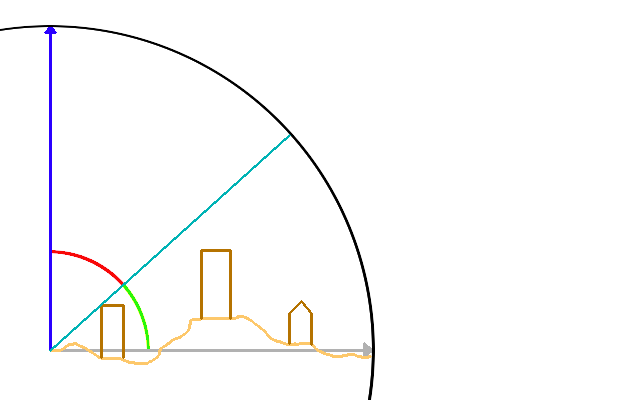
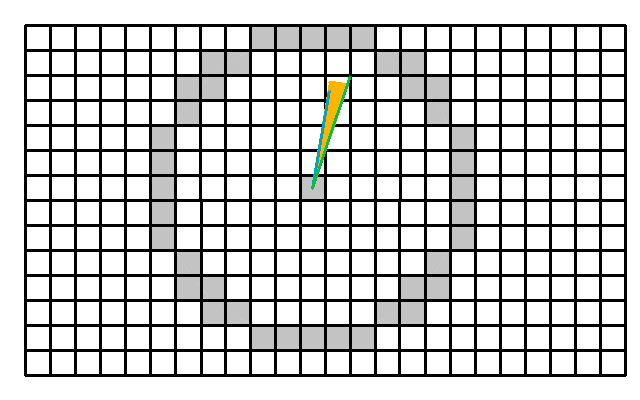
Two consecutive rays are casted. Each ray results in a maximum sky view angle.
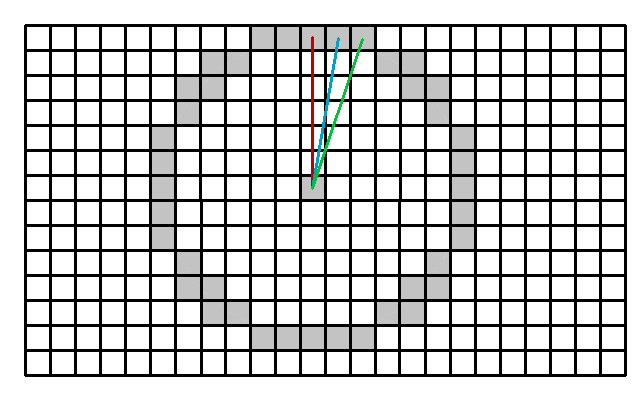
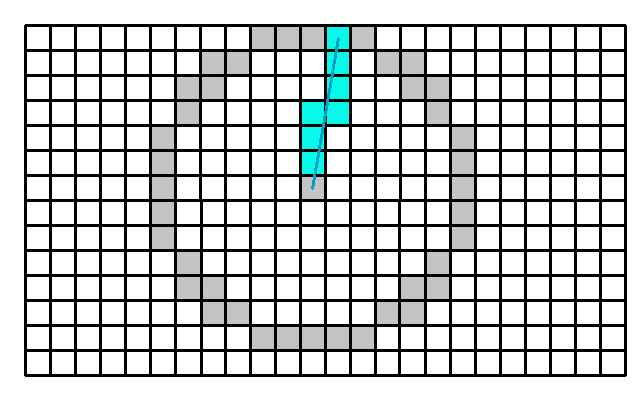
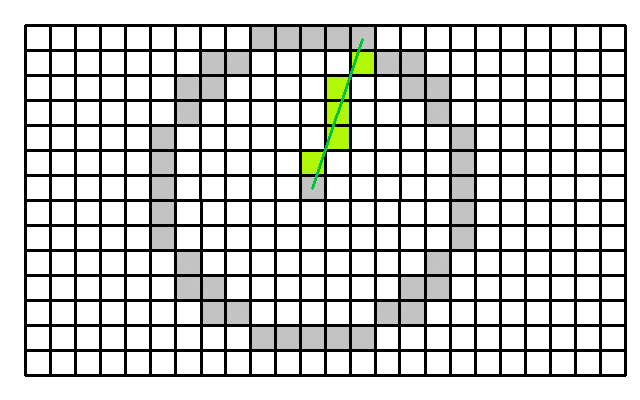
The sections are formed by each consecutive pair of direction rays. As you can see from the image, the amount of rays is dependent on the grid size and the search area. Each ray is processed only once. From the side you can see the maximum view angle, based on the buildings, foliage and terrain height. The projected section radius (in dark green) is obtained by projecting the view ray onto the horizontal plane.
The sky view section is formed by the two consecutive projected rays.
We use the average projected ray length from these two rays r1 and r2 to calculate the area:
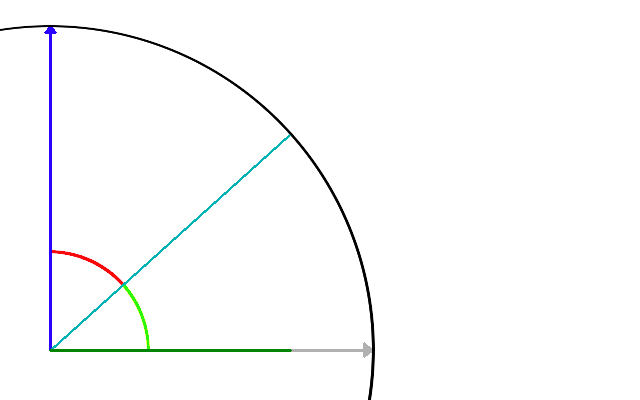
angle = acos(xr1 xr2, yr1 yr2)
r1,2 = (r1 + r2)/2;
area = angle / (2 π) π r1,22
The sky view area is then calculated as the sum of the areas of sky view sections.
With the sky view area, the sky view factor can be calculated by dividing the sky view area by the area of the circle of the horizontal plane.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sum_{1}^n area_i }, \pi r^2 }}
Notes
- The size of the dome and sky circle on the horizontal plane do not matter. They can simply be a unit sphere and circle. Only the angle between the ray and the horizontal plane determine the sky view sections.