Radial well aquifer benchmark (Water Module)

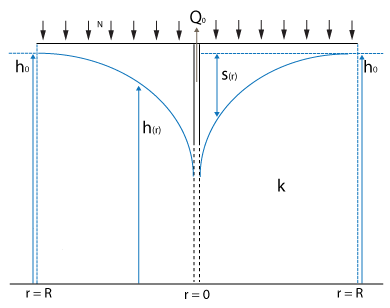
This benchmark demonstrates a situation where a well is extracting ground water. A characteristic ground water level curve will form over time.

Formulas

Stationary lowering of the ground water table in a closed water transmissive layer can be described by the following formula

$\phi (r)-\phi _{0}={\frac {Q_{0}}{2\pi \cdot kD}}\ln {\left({\frac {r}{R}}\right)}$

where:

$phi_{0}$: stable water level at the considered stable water table edge

$phi(r)$: water level between the considered stable water table edge and the well

$kD$: transmissivity of the aquifer in m² / day

$r$: distance to the well

$R$: distance of the considered stable water table edge to the well

$Q_{0}$: amount of water pumped out in m³ / day

Setup

We use the following setup in our tests. The grid size used is 51 by 51, with a configurable cell size of $dx$ in meters. There is one underground outlet, which pumps water away continuously with a default amount per second.

The terrain height is set to 0 meters (datum).

The outlet is placed on the cells x = 25 and y = 25 as an inlet with a negative inlet.

INLET Q is set to ${\frac {-Q_{0}}{3600*24}}$

UNDERGROUND is set to true (1.0) to place the outlet below the surface.

To stabilized the water levels on the edges of the test case , an additional underground inlet is used. It is located on all cells equal to or further away than the chosen R. This inlet is configured as followed:

Inlet Q set to 0, such that is unlimited.

UNDERGROUND is set to true (1.0) to place the outlet below the surface.

UPPER_THRESHOLD set to -2 m.

LOWER_THRESHOLD set to -2 m.

The ground bottom distance is configured as 10 meters, which places the bottom at -10 meters (datum).

The water storage fraction is set to 0.25.

An aquifer can be added to configure the kD value used in the test.

The simulation is run for 64 days with 0 rainfall, which is configured in the weather's rain attribute as: $[64\cdot 24\cdot 3600,0]$

Test results

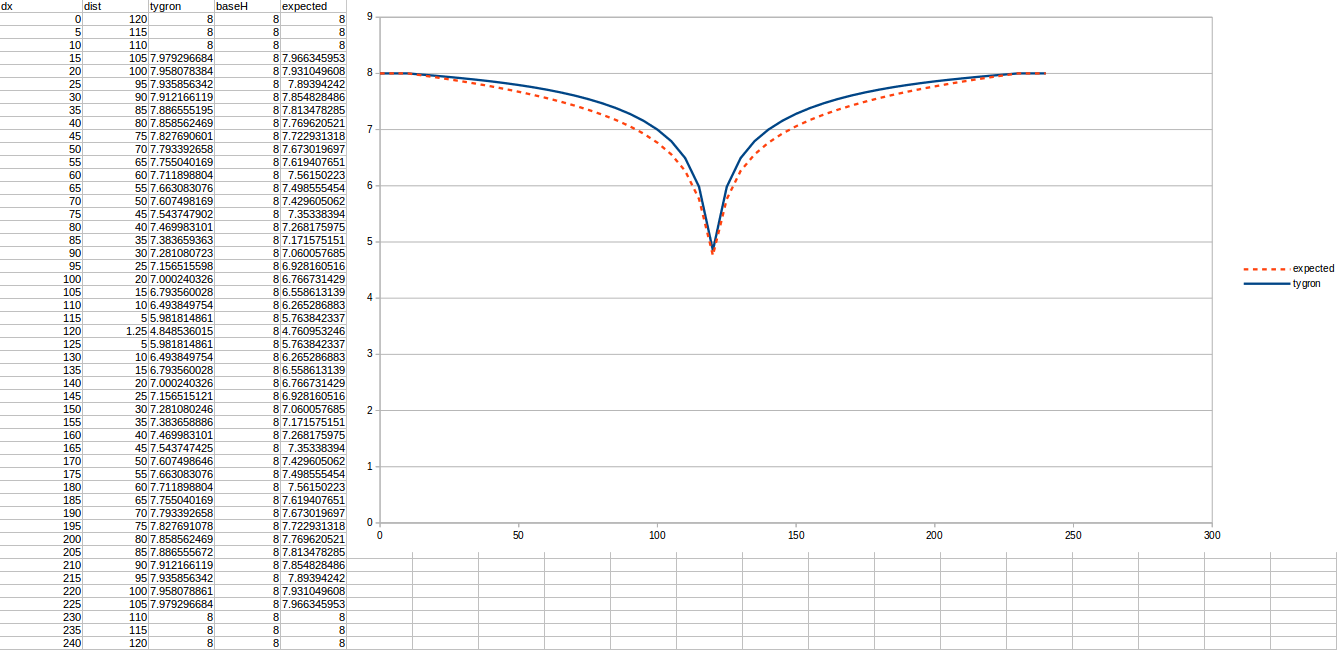
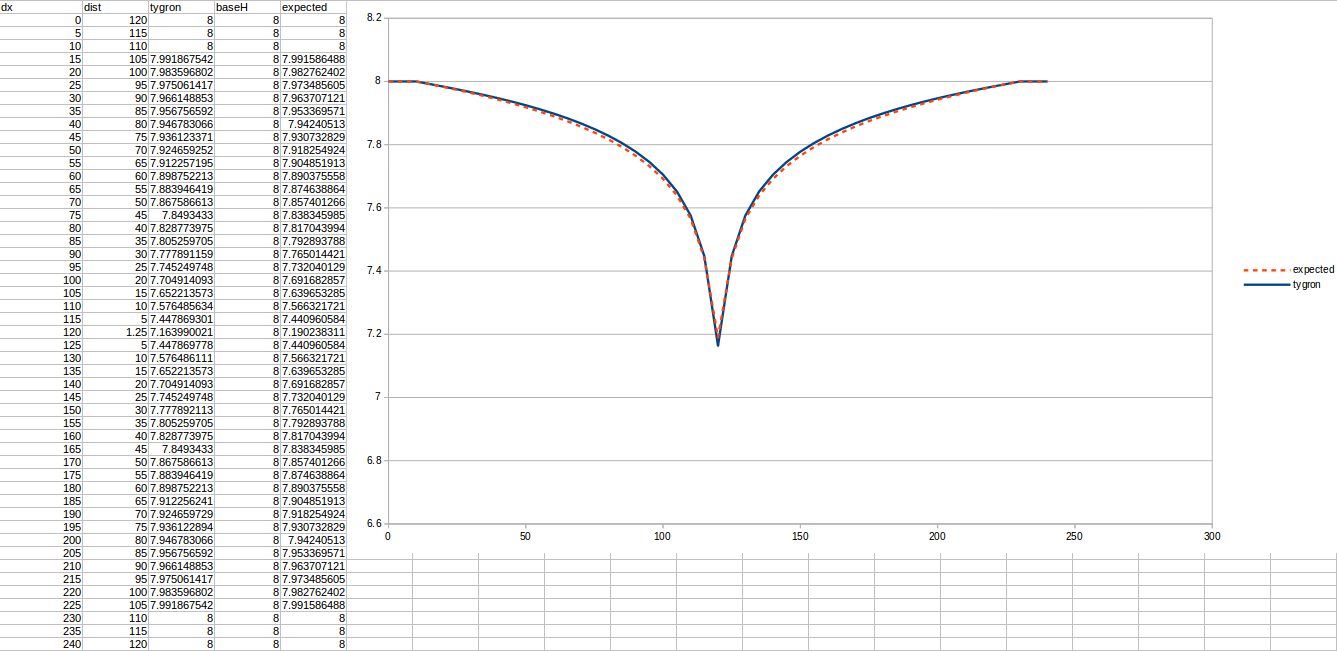
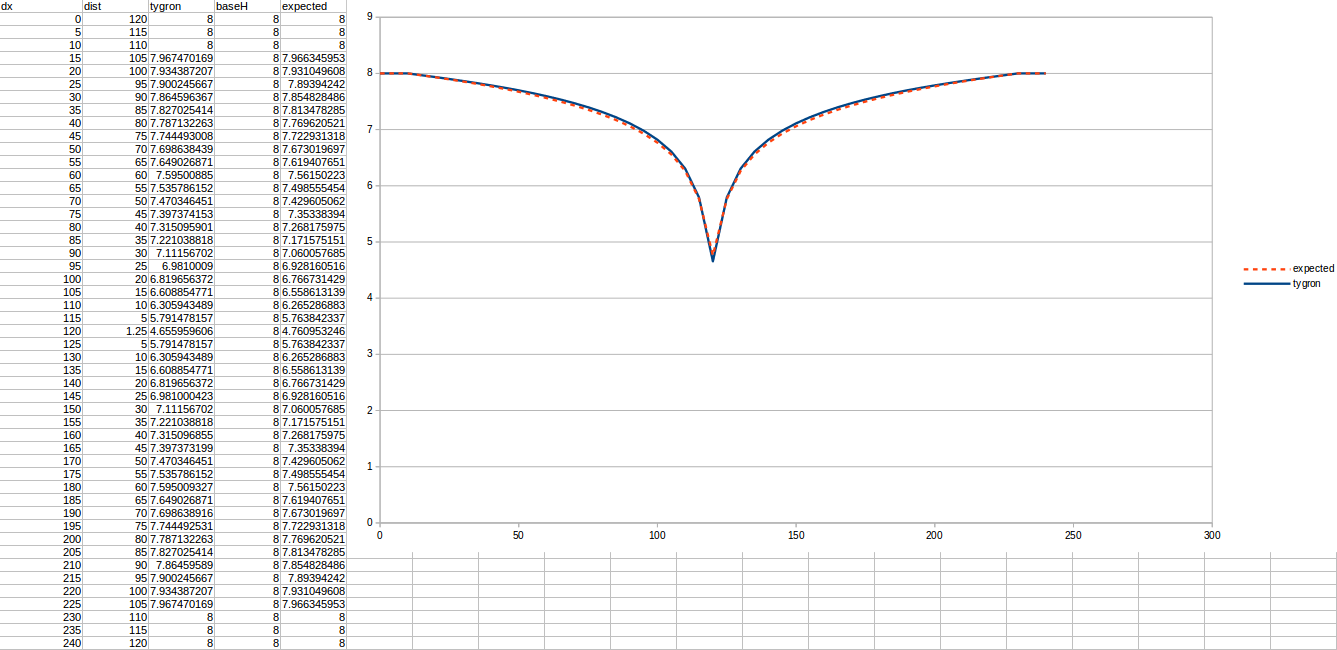
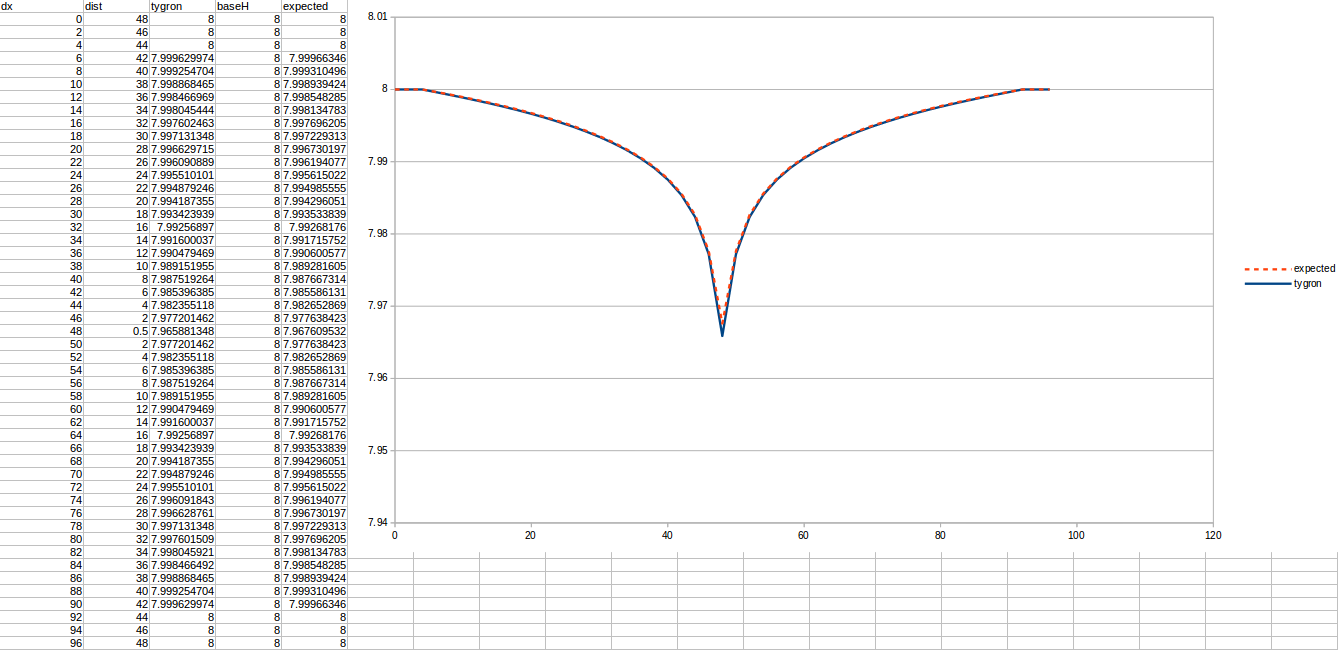
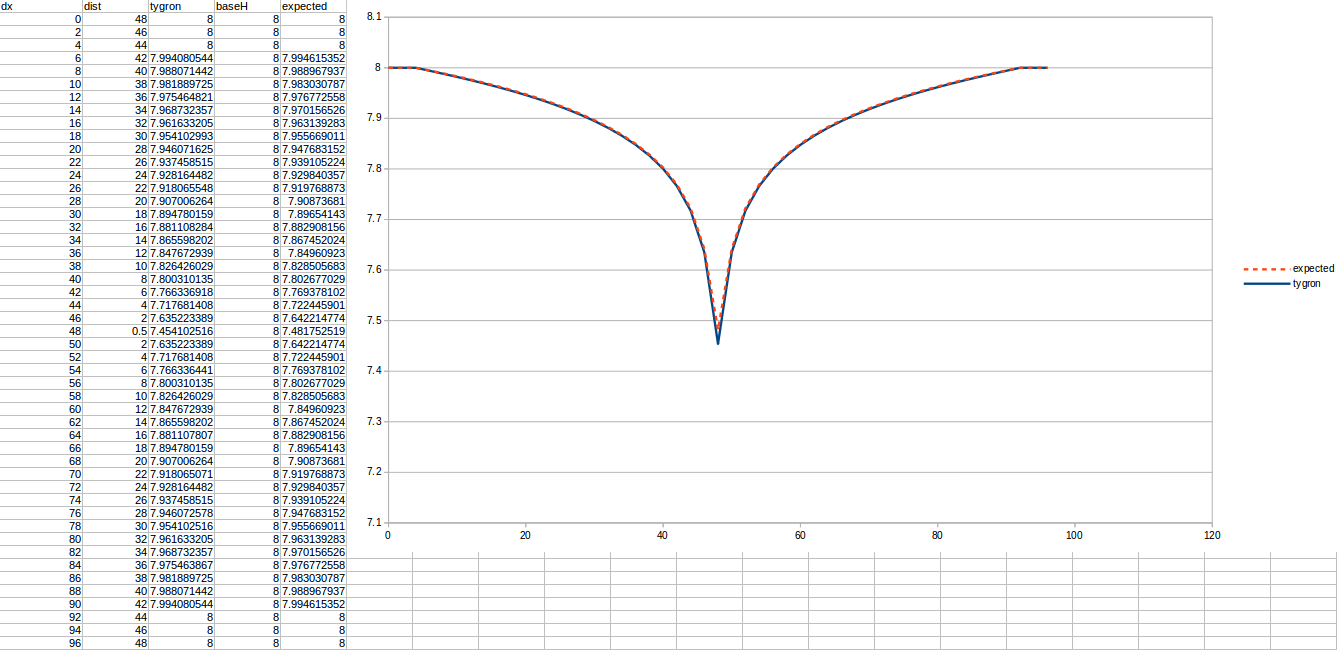
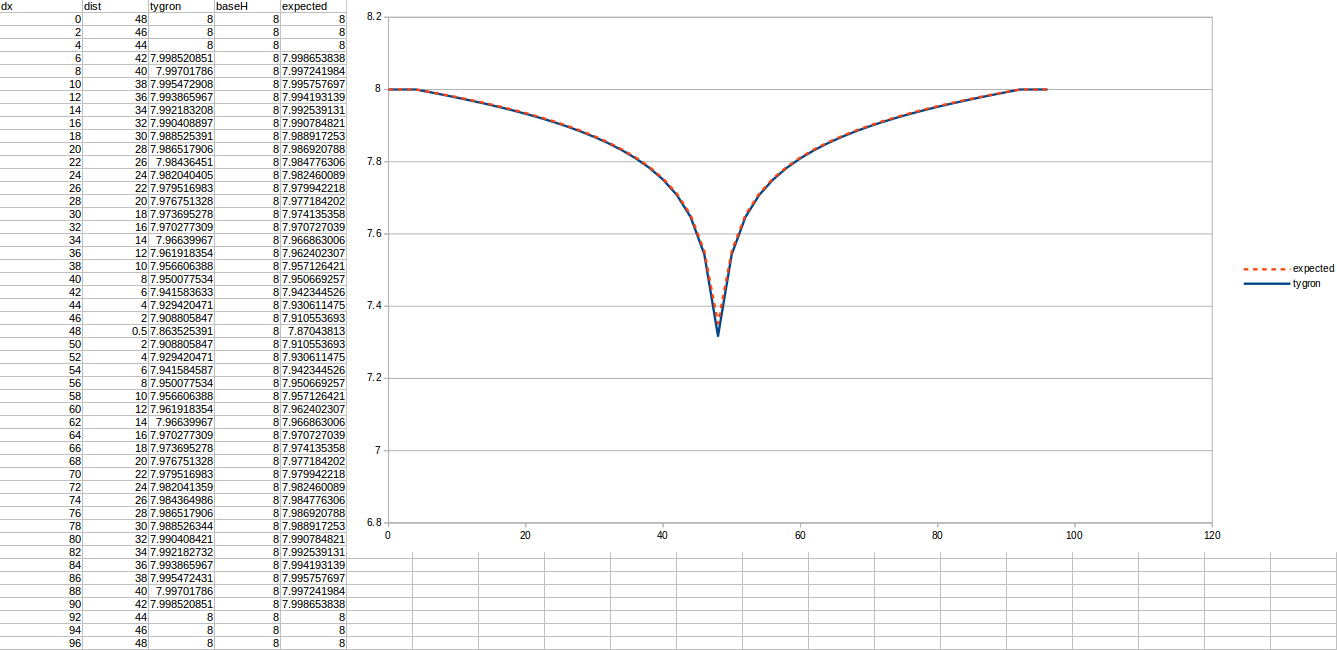
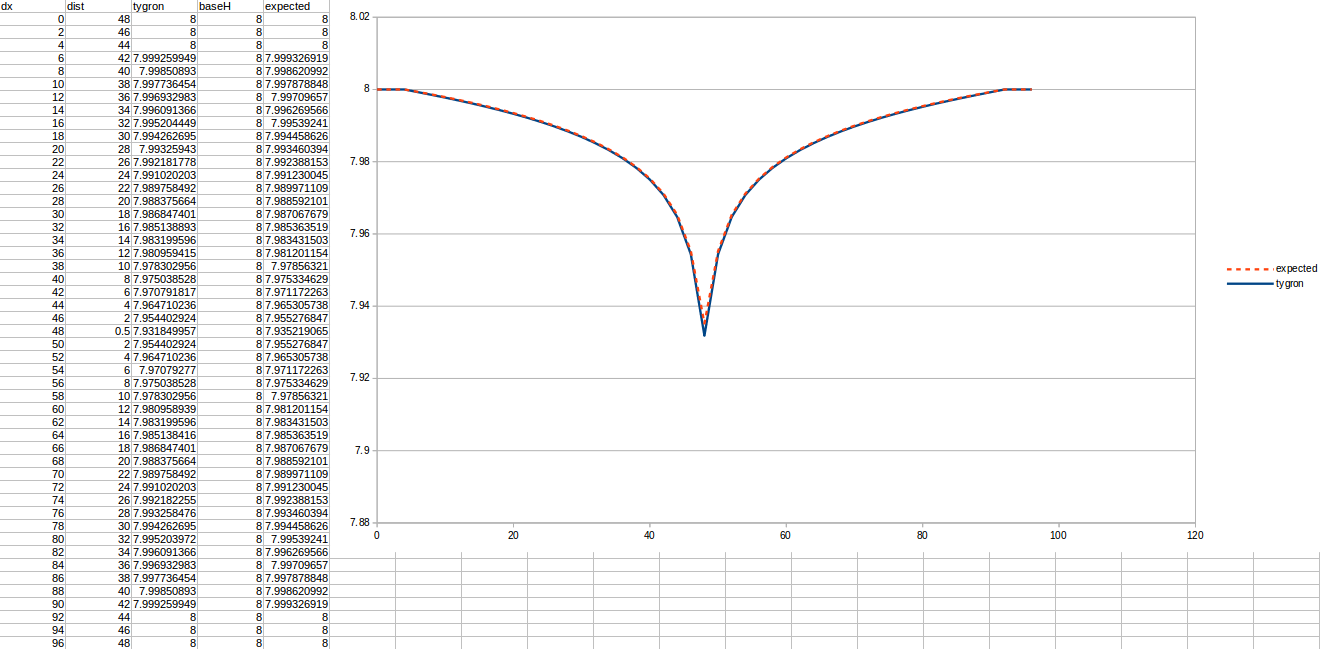
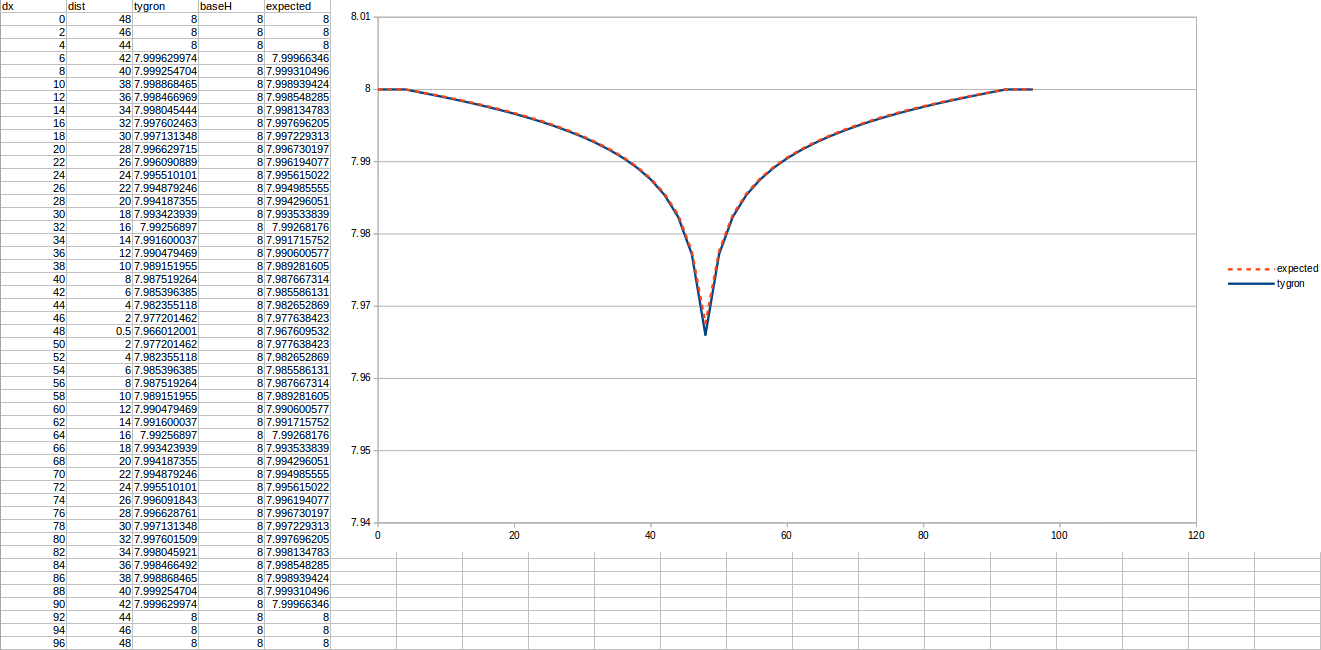
Important in all these tests is the chosen R, which is the distance to the well that is considered a stable water level. Additionally, the measurements are done relative to the bottom boundary, which is situated 10 meters below the surface.

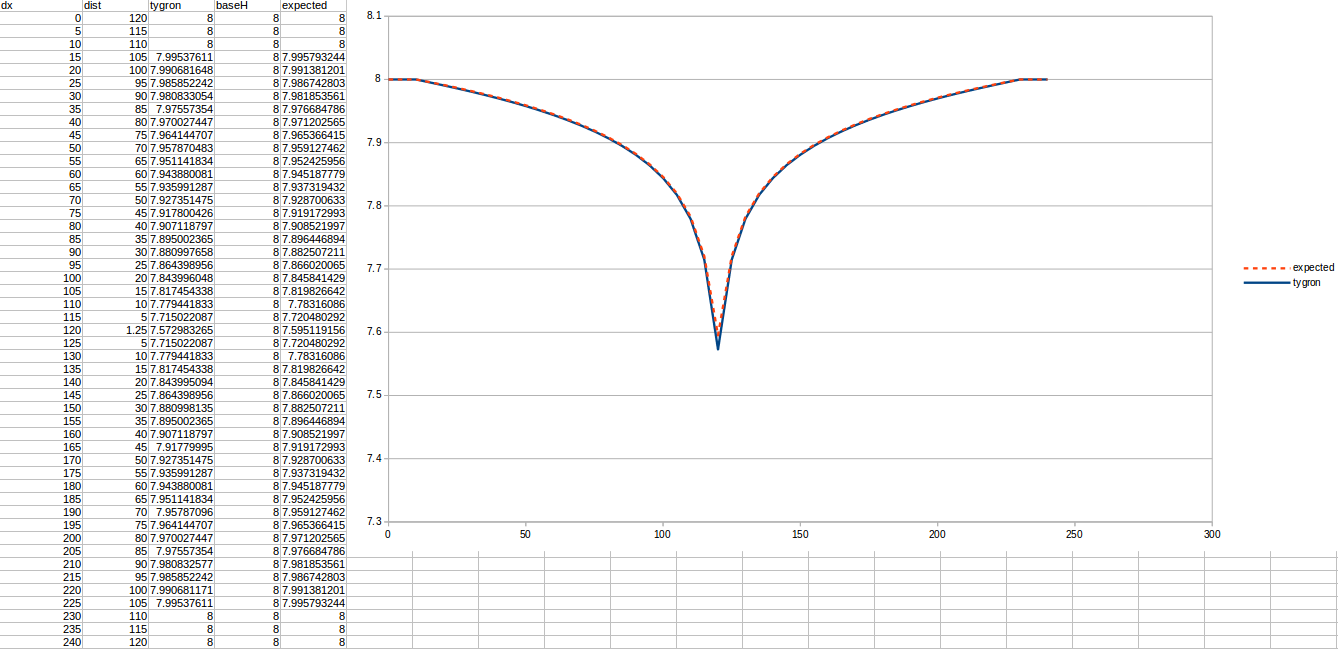
Test case 1

cell size: 5 m;

$kD$: 88 m²/day;

$R$: 110;

$Q_{0}$: 50;

Simulation days $n$: 64 days;

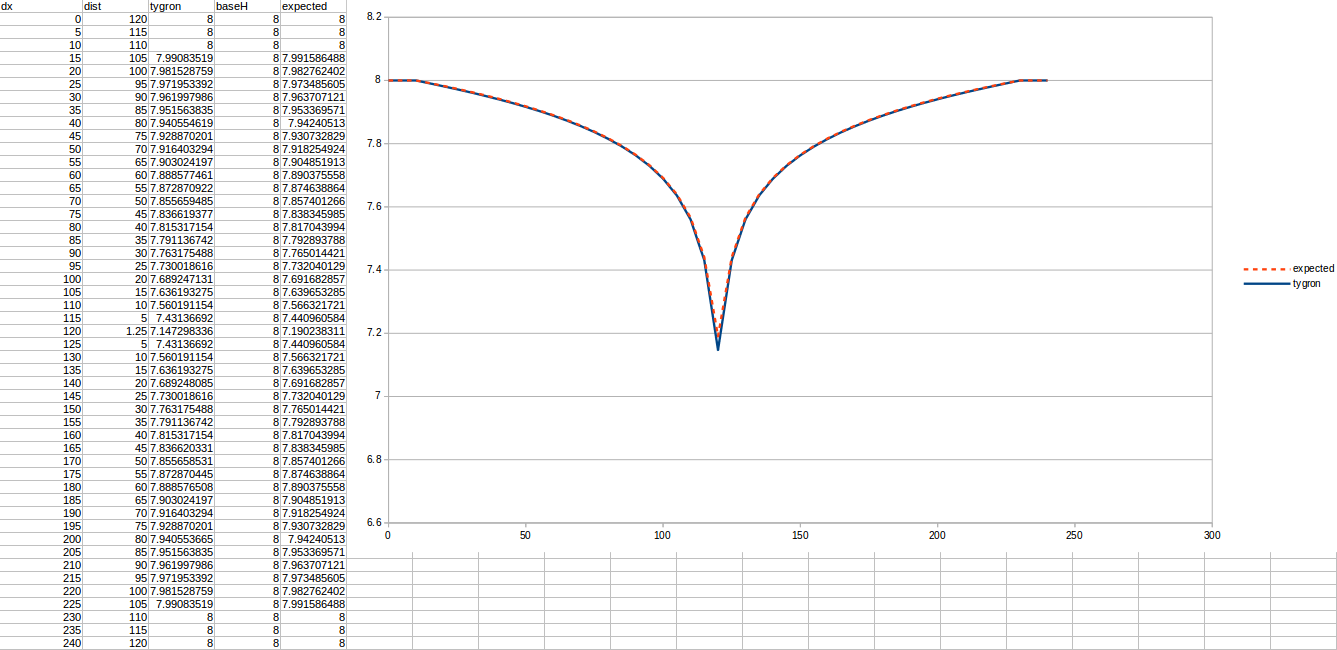
Test case 2

cell size: 5 m;

$kD$: 44 m²/day;

$R$: 110;

$Q_{0}$: 50;

Simulation days $n$: 64 days;

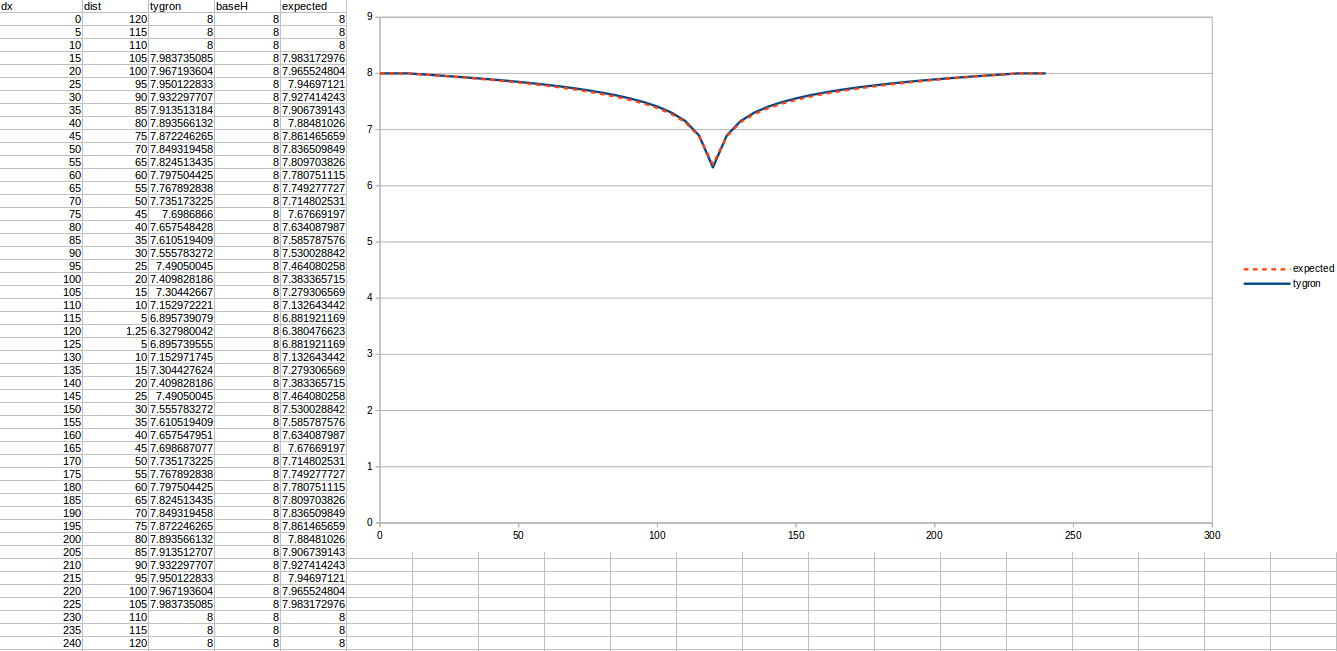
Test case 3

cell size: 5 m;

$kD$: 22 m²/day;

$R$: 110;

$Q_{0}$: 50;

Simulation days $n$: 64 days;

Test case 4

cell size: 5 m;

$kD$: 11 m²/day;

$R$: 110;

$Q_{0}$: 50;

Simulation days $n$: 64 days;

Test case 5

cell size: 5 m;

$kD$: 22 m²/day;

$R$: 110;

$Q_{0}$: 25;

Simulation days $n$: 64 days;

Test case 6

cell size: 5 m;

$kD$: 22 m²/day;

$R$: 110;

$Q_{0}$: 100;

Simulation days $n$: 64 days;

Test case 7

cell size: 2 m;

$kD$: 22 m²/day;

$R$: 110;

$Q_{0}$: 1;

Simulation days $n$: 64 days;

Test case 8

cell size: 2 m;

$kD$: 22 m²/day;

$R$: 110;

$Q_{0}$: 16;

Simulation days $n$: 64 days;

Test case 9

cell size: 2 m;

$kD$: 22 m²/day;

$R$: 110;

$Q_{0}$: 4;

Simulation days $n$: 64 days;

Test case 10

cell size: 2 m;

$kD$: 44 m²/day;

$R$: 110;

$Q_{0}$: 4;

Simulation days $n$: 64 days;

Test case 11

cell size: 2 m;

$kD$: 88 m²/day;

$R$: 110;

$Q_{0}$: 4;

Simulation days $n$: 64 days;

References

Water Module

Tutorials

Overview

Theory

Benchmarks