Wind calculation model (Heat Overlay)
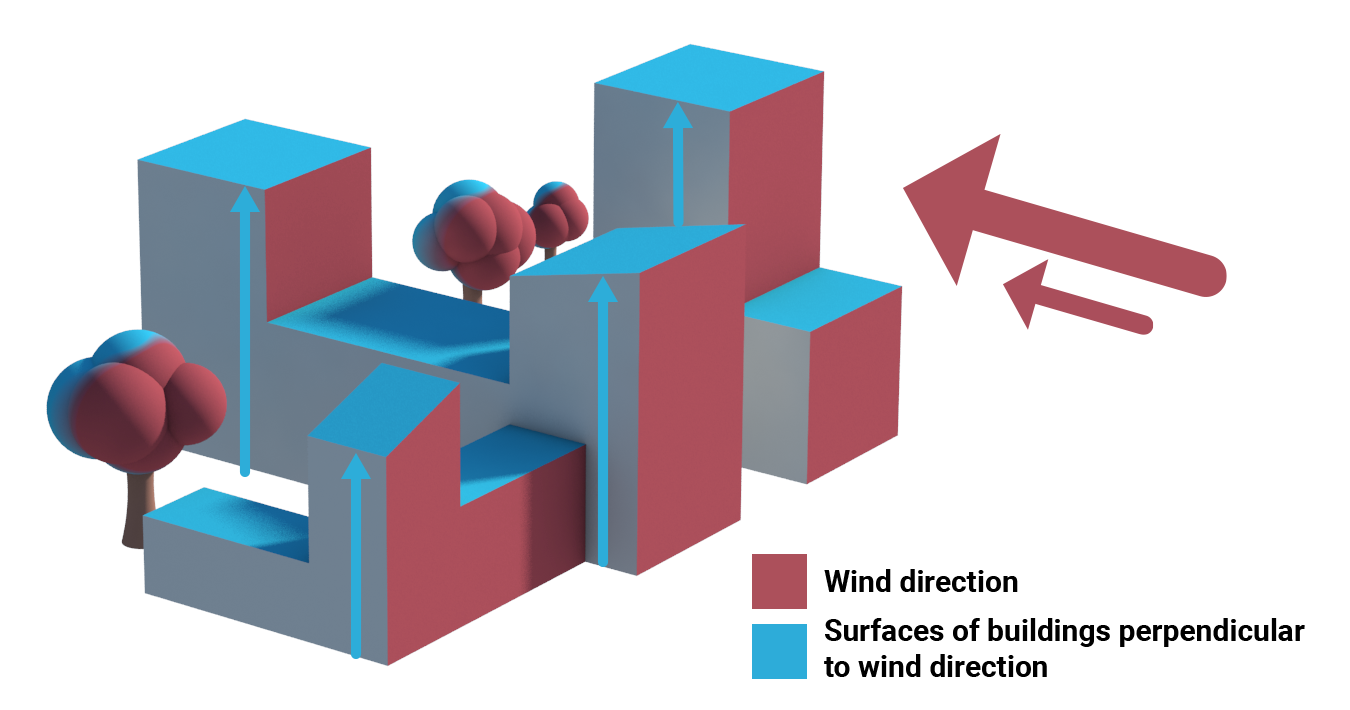
The wind speed on street level (1.2 meter) is calculated using a translation of the 10 meter wind speed measured at a weather station. A single reduction field per wind direction can be calculated, which in turn can be multiplied with the 10 meter wind speed to obtain the wind speed at street level. The calculation model is based on the McDonald (2000) method for wind in cities. It uses the vertical surfaces of buildings perpendicular to the wind direction to determine in what way the wind speed is slowed down. The DPRA Heat stress report has extended this method with perpendicular vertical tree surfaces as well.
Implementation
The calculation implemented in the Tygron Platform differs from the implementation described by the DPRA Heat stress report. Specifically, rather than performing the described cubic interpolation from coarse grids to more detailed grids, all operation are done on a detailed grid.
Averaging window
- Main article: Average calculation model (Heat Overlay)
The average wind speed is based on an average of wind speeds across a larger area. The window for averaging is established based on wind speed and direction. For slow wind speeds (below 1.5m/s), a wind speed of 175x175m is used. For high wind speeds, a window of 280x140m if used.
Per grid cell
Per grid cell in the averaging window:
- Determine the average obstacle height per square meter. Buildings and trees lower than 2 meters are not taken into account. It is divided by the area of the search window.
- Determine the average vertical building surface perpendicular to the wind direction. Again this is divided by the area of the search window.
- Determine the frontal surface compactness factor , separately for buildings and trees. Combine these to obtain .
- Determine the average height of trees, with 4 meters as minimum value.
- Using these values, select the correct formula parameters from the McDonald 2000 table for , , , and
- Using the obtained parameters, calculate the wind translation factor.
- Obtain the wind speed at by multiplying the wind translation factor with the measured at the weather station. Since the wind speed can still be too low, apply a correction formula to to obtain the end result.
Determine average object height
For each cell in the wind direction window the average obstacle height of the buildings and foliage are calculated. Only foliage and buildings with a minimum height of 4.0 area taken into account. If no obstacles were present, the average height will still be at the minimum of 4 meters.
Determine average vertical surface perpendicular to wind direction
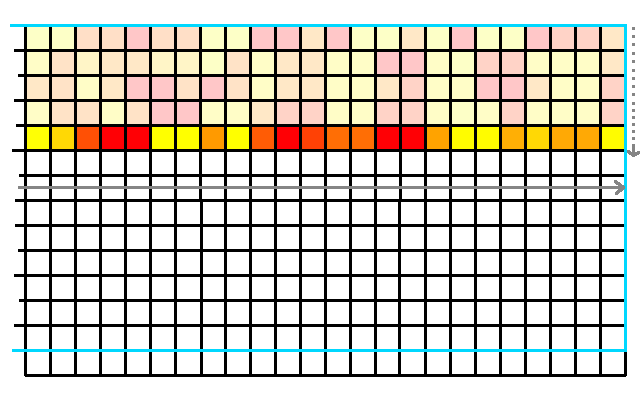
For each strip in the direction of the wind:
Check if the height of buildings is higher than the previous cell:
if and
where is the width of a cell. So we only calculate additional heights.
Next, divide by n, the amount of cells visited to obtain .
For the same process is repeated, but then with foliage heights instead of Building heights.
Determine the combined frontal surface compactness factor
First, calculate and in a similar way, described in step 2.
Next, calculate the using the and .
.
Determine average tree height
Calculate the average obstacle height , where a minimum height threshold of 4 is used. This means it is always at least 4 meters high.
Select applicable formula parameters from McDonald 2000 table
Select the function parameters , , , and from the table using and :
| 0.05 (<0.08) | 0.066 | 2 | 0.048 | -0.35 | 0.56 |
| 0.11 (<0.135) | 0.26 | 2.5 | 0.071 | -0.35 | 0.50 |
| 0.16 (<0.18) | 0.32 | 2.7 | 0.084 | -0.34 | 0.48 |
| 0.20 (<0.265) | 0.47 | 1.5 | 0.08 | -0.56 | 0.66 |
| 0.33 (>=0.265) | 0.57 | 1.2 | 0.077 | -0.85 | 0.92 |
Caclulate wind translation factor
Calculate the translated intermediate wind speeds:
Obtain final corrected wind speed
The obtained wind speed can be too low. Therefore it is corrected with the following formula:
This corrected value is used in the formula for PET.
Improved wind model
The roughness of the frontal surface affects wind speed. In the original DPRA Heat stress report, the frontal surface is derived from very basic tree shapes. However, when utilizing more detailed foliage data, such as AI-detected individual trees, the frontal surface becomes excessively large. This result is less wind and an increase in heat around woods.
To address this issue, a WIND_DECLINE_ANGLE can be applied to smooth the wind flow, leading to a more accurate representation of the frontal surface and producing more realistic values in wooded areas or parks.
Notes
- The model currently only calculates the adjusted wind speeds in the 4 cardinal directions: north, east, south, west.
See also




